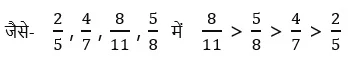संख्या पद्धति किसे कहते हैं? What is The Number System?

संख्या पद्धति (Number System)

वह पद्धति जिसमें विभिन्न संख्याओं तथा उनके गुणों का अध्ययन किया जाता है, “संख्या पद्धति" कहलाती है। या किसी भौतिक राशि के परिणामों को बोध कराने के लिए जिस पद्धति का प्रयोग किया जाता हैं, संख्या पद्धति" कहलाती है।

अंक (Digit) 

गणित में 0 से लेकर 9 तक के संकेतों को अंक कहते हैं इनकी इनकी संख्या 10 होती है। जैसे - 0, 1, 2, 3, 4, 5, 6, 7, 8,9. 

संख्या किसे कहते हैं?

संख्या (Number) 

एक से अधिक अंकों को मिलाने पर संख्या का निर्माण होता है इनकी संख्या अनन्त होती है जैसे- 123,241,2375,855,5833.

संख्याएँ कितने प्रकार की होती हैं?

संख्याओं के प्रकार (Types of Numbers) 

प्राकृतिक संख्या (Natural Number)

गिनती की संख्याओं को प्राकृतिक संख्या कहते हैं अथवा ऐसी संख्या जो 1 से शुरू होकर अनन्त तक चलती है, प्राकृतिक संख्याएँ कहलाती है।

• प्राकृतिक संख्या को N से प्रकट करते हैं।
• 1 सबसे छोटी प्राकृतिक संख्या है।

पूर्ण संख्या किसे कहते हैं?

पूर्ण संख्याएँ (Perfect Number)

प्राकृतिक संख्याओं में शून्य को सम्मिलित करने पर जो संख्याएँ प्राप्त होती हैं उन्हें पूर्ण संख्याएँ कहते

जैसे- 0, 1,2,3,4,5,6,7,8,9

• पूर्ण संख्या को W से प्रकट करते हैं।
• 0 सबसे छोटी पूर्ण संख्या है।
• 0 ऐसा अंक है जो W को N से अलग करता है।
• सभी प्राकृतिक संख्याएं पूर्ण संख्या है, लेकिन सभी पूर्ण संख्या प्राकृतिक संख्या नहीं है।

नोट – पूर्ण संख्या ऐसी संख्याएँ जिनके गुणनखण्डों का योग (स्वयं को छोडकर) करने पर वही संख्या प्राप्त हो, पूर्ण संख्या कहलाती है

उदाहरण- 6, 28

• 28 के गुणनखंड = 1x28, 2x14, 4x7 = 1, 2, 4, 7, 14, 28 = 1+2+4+7+14-28

पूर्णांक संख्याएँ किसे कहते हैं? 

पूर्णांक संख्याएँ (Integers Number)

प्राकृत संख्याओं में शून्य एवं ऋणात्मक संख्याओं को भी सम्मिलित करने पर जो संख्याएँ प्राप्त होती हैं, उन्हें पूर्णांक संख्याएँ' कहते हैं। जैसे-   -1, -2, -3, 0, 1,2,3,

• पूर्णांक संख्याओं को Z से प्रकट करते हैं।
• Zealean नामक जर्मन गणितज्ञ ने सबसे पहले पूर्णांक संख्याओं के बारे में बताया ।
• 0 समस्त ऋणात्मक पूर्णांक संख्याओं से बड़ा होता है तथा समस्त धनात्मक पूर्णांक संख्याओं से छोटा होता है।

सम संख्याएँ क्या हैं?

सम संख्याएँ (Even Numbers)

वे संख्याएँ जो 2 से पूर्णतः विभाजित हो जाती हैं उन्हें सम संख्याएँ' कहते हैं। इस प्रकार 2, 4, 8,6, 26....... आदि सम संख्याएँ हैं।

• सम संख्याओं को E से प्रकट करते है।
• 2 सबसे छोटी सम संख्या है।
• सम संख्याओं का इकाई अंक 0, 2, 4, 6 या 8 होता है।
• 0 एक सम संख्या है। 

विषम संख्याएँ क्या हैं?

विषम संख्याएँ (Odd Numbers)

वे संख्याएँ जो 2 से पूर्णतः विभाजित नहीं होती हैं उन्हें विषम संख्याएँ कहते हैं। जैसे- 1, 3, 5, 11, 17, 29, 39 ....... आदि 'विषम संख्याएँ' हैं। 

अभाज्य संख्याएँ किसे कहते हैं?

अभाज्य संख्याएँ (Prime Numbers)

वे संख्याएँ जो स्वयं और 1 के अतिरिक्त अन्य किसी भी संख्या से विभाजित नहीं हो उन्हें 'अभाज्य संख्याएँ कहते हैं। जैसे- 2,3,7, 11, 13, 17......... आदि 'अभाज्य संख्याएँ हैं।

• अभाज्य संख्याओं को रूढ़ संख्याएँ भी कहते है
• 2 सबसे छोटी अभाज्य संख्या है
• 2 एक मात्र ऐसी सम संख्या है, जो अभाज्य संख्या भी है।
• 3 सबसे छोटी विषम अभाज्य संख्या है।
• 1 से 100 तक अभाज्य संख्याएँ - 25 है।

कोई संख्या अभाज्य है या नही इसकी जाँच कैसे करते हैं?

कोई संख्या अभाज्य है या नही इसकी जाँच करने के लिए निम्नवत बिन्दुओं को ध्यान रखना चाहिए-

• उस संख्या से छोटी सबसे निकट पूर्ण वर्ग संख्या का वर्गमूल ज्ञात करें
• उस वर्गमूल से छोटी सभी अभाज्य संख्याओं का भाग दी गई संख्या में दें
• यदि किसी अभाज्य संख्या का भाग नही जाता है तो दी गई संख्या अभाज्य संख्या है - जैसे - 331
• 331 से छोटी निकटतम पूर्ण वर्ग संख्या - 324
• 331 का वर्गमूल = 18
• 18 से छोटी अभाज्य संख्याएं =2, 3, 5, 7, 11, 13, 17
• 331,18 से छोटी किसी भी अभाज्य संख्या से विभाजित नहीं है अतः 331 अभाज्य संख्या है

भाज्य संख्याएँ क्या होती हैं?

भाज्य संख्याएँ (Composite Number)

वे संख्याएँ जो स्वयं और 1 के अतिरिक्त अन्य किसी संख्या से पूर्णतः विभाजित हो जाती है तो उसे भाज्य संख्या कहते हैं। जैसे- 4, 6, 8, 9, 10,

• सबसे छोटी भाज्य संख्या 4 है
• सबसे छोटी विषम भाज्य संख्या- 9 है।
• 1 से 100 तक भाज्य संख्याएँ – 74 है।

परिमेय संख्या किसे कहते हैं?

परिमेय संख्याएँ (Rational Number)

वे संख्याएँ जिन्हेंp/q के रूप में लिखा जा सके परिमेय संख्याएँ कहलाती हैं जहाँp और q दोनों पूर्णांक हो लेकिन कभी शून्य न हो। जैसे- 4,3/4,0......... आदि परिमेय संख्याएँ हैं।

• परिमेय संख्याओं को "Q" से प्रकट करते है।

अपरिमेय संख्या किसे कहते हैं?

अपरिमेय संख्याएँ (Irrational Numbers)

वे संख्याएँ जिन्हेंp/q के रूप में न लिखा जा सके अपरिमेय संख्याएँ कहलाती है। जहाँ p और q दोनों पूर्णांक हो लेकिन कभी शून्य न हो। जैसे-  √7, √5, 2+√2, π … आदि अपरिमेय संख्याएँ हैं।

वास्तविक संख्या किसे कहते हैं?

वास्तविक संख्याएँ (Real Numbers)

वे संख्याएँ जो या तो परिमेय हैं अथवा परिमेय और अपरिमेय संख्याओं के समूह को वास्तविक संख्या कहते है। वास्तविक संख्याओं को R से सूचित किया जाता है।  जैसे- 8, 6, √5, 3/5… आदि वास्तविक संख्याएँ हैं।

सह-अभाज्य संख्या किसे कहते हैं?

सह-अभाज्य संख्याएँ (Co-Prime Numbers)

ऐसी संख्याओं के जोड़े जिनके गुणनखण्डों में 1 के अतिरिक्त कोई भी उभयनिष्ठ गुणनखण्ड न हो उन्हें 'सह-अभाज्य संख्याएँ कहते हैं। जैसे- 16,21 में 1 के अतिरिक्त अन्य कोई उभयनिष्ठ गुणनखण्ड नहीं है।

• वे संख्या युग्म जिनका महत्तम समापवर्तक(HCF) 1 हो 
• इसमें संख्या युग्म केवल अभाज्य संख्याओं के ही बनाते हैं।

आपेक्षित अभाज्य संख्या किसे कहते हैं?

आपेक्षित अभाज्य संख्या (Relatively Prime Number)

• वे संख्या युग्म जिनका महत्तम समापवर्तक(HCF) 1 हो ।
• इसमें संख्या युग्म भाज्य, अभाज्य संख्याओं के बनाते हैं।

युग्म-अभाज्य संख्या किसे कहते हैं?

युग्म-अभाज्य संख्याएँ (Pair Prime Numbers)

ऐसी अभाज्य संख्याएँ जिनके बीच का अंतर 2 हो 'युग्म-अभाज्य संख्याएँ' कहलाती हैं। युग्म-अभाज्य संख्याएँ हैं।जैसे-  (11, 13), (5,7),(17,19), (29,31), (59,61), (71,73) 

रामानुजम संख्या किसे कहते हैं?

रामानुजम संख्या (Ramanujan Number)

वह छोटी से छोटी संख्या जिसे दो अलग - अलग प्रकार से घनों के योग के रूप में लिख जा सकता है, रामानुजम संख्या कहलाती है 

अत्रिभाज्य संख्याएँ क्या होती हैं?

अत्रिभाज्य संख्याएँ (Prime Triplet Number)

वे तीन प्राकृतिक संख्याएँ जिनका महत्तम समापवर्तक (H.C.F) 1 हो, अत्रिभाज्य संख्याएँ कहलाती है।

जैसे- 8, 9 तथा 25

भिन्न (FRACTIONS)

यदि किसी संख्या कोp/q के रूप में जहाँp और व पूर्णांक हैं तथा 0 लिखा जाये तो ऐसी संख्या को भिन्न कहते हैं। भिन्न में भाज्य को एक रेखा के उपर तथा भाजक को रेखा के नीचे लिखा जाता है, ऊपर की संख्या अर्थात भाज्य को अंश तथा नीचे की संख्या अर्थात भाजक को हर कहा जाता है। 14 आदि भिन्न के उदाहरण हैं जिसमें 1,4,6 अंश तथा 3,5,7 हर हैं।

उदाहरण- भिन्न एक ऐसी संख्या है जो किसी सम्पूर्ण चीज़ का कोई भाग निरुपित करती है। जैसे: एक सेब के चार भाग किये जाते है जिनमें से उनके एक हिस्से को निकाल दिया गया है तो उसे ¼ के रूप में प्रदर्शित किया जाता हैं. जबकि शेष बचे भाग को ¾ के रूप में इंगित किया जाता हैं।  

भिन्न कितने प्रकार की होती हैं?

भिन्न के प्रकार

उचित भिन्न- यदि भिन्न का अंश हर से कम हो, तो भिन्न को उचित भिन्न कहते हैं।

जैसे 2/4, 2/6, 5/10 इत्यादि। 

अनुचित भिन्न- यदि भिन्न का अंश हर से बड़ा हो तो भिन्न को अनुचित भिन्न कहते हैं।

जैसे-15/5, 6/12, 16/8 .... इत्यादि। 

मिश्र भिन्न- यदि भिन्न एक पूर्णांक तथा भिन्न से मिलकर बनी हो तो भिन्न को मिश्र भिन्न कहते हैं।

जैसे 2,325,..... इत्यादि।

दशमलव भिन्न किसे कहते हैं?

दशमलव भिन्न

वे भिन्न जिनके हर 10, 100 या 1000 इत्यादि हो, तो दशमलव भिन्न कहलाते हैं।

जैसे- 7/10, 11/100, 12/1000 ...... इत्यादि।

• 10,100 इत्यादि हरों वाली भिन्नों को दशमलव बिंदु का प्रयोग करके एक विशेष रूप में लिखा जा सकता है। इस रूप में ये दशमलव संख्याएँ कहलाती हैं।

• दशमलव बिन्दु के ठीक बाद वाले स्थान (अर्थात् दशांश के स्थान) का स्थानीय मान 1/10

होता है, उससे अगले स्थान (अर्थात् शतांश के स्थान) का स्थानीय मान 1/100होता है, इत्यादि।

• दशमलव संख्याओं की तुलना स्थानीय मान की धारणा का प्रयोग करते हुए की जा सकती है और फिर उन्हें आरोही या अवरोही क्रम में व्यवस्थित किया जा सकता है।

• दशमलवों को, बराबर दशमलव स्थानों के रूप में लिखकर जोड़ा (या घटाया) जा सकता है।

• मापनों के विभिन्न मात्रकों, जैसे मुद्रा (या धन राशि), लंबाई, भार, इत्यादि को दशमलव रूप में बदल कर, फिर उन्हें जोड़कर (या घटाकर) दैनिक जीवन की अनेक समस्याओं को हल किया जा सकता है। 

वितत भिन्न- सामान्य तौर पर किसी भिन्न के हर या कभी-कभी अंश में किसी संख्या के जोड़ने या घटाने से बनने वाले भिन्न को वितत भिन्न कहते हैं।

भिन्नों की तुलना कैसे करते हैं?

भिन्नों की तुलना

यदि दी गई भिन्नों के हर समान हो, तो सबसे बड़े अंश वाली संख्या बड़ी होगी।

यदि दी गई भिन्नों के अंश समान हो, तो सबसे छोटे हर वाली संख्या बड़ी होगी।

यदि दी गई भिन्नों में उनके अंशों और हरों का अंतर समान हो, तो सबसे छोटे अंश वाली संख्या सबसे बड़ी होगी, जबकि अंश हर से बड़ा है।

यदि दी गई भिन्नों में उनके अंशों और हरों का अंतर समान हो, तो सबसे बड़े अंश वाली संख्या सबसे बड़ी होगी, जबकि अंश, हर से छोटा है।

तिर्यक विधि से भिन्नों की तुलना कैसे करते हैं?

तिर्यक विधि द्वारा भिन्नों की तुलना

यह भिन्नों की तुलना के लिए एक संक्षिप्त विधि है। इस विधि के द्वारा हम सभी प्रकार के भिन्नों की तुलना कर सकते हैं। उदाहरणस्वरूप इस विधि द्वारा 5/9 और 4/7 की तुलना इस प्रकार करेंगे।

संख्याओं का दशमलव प्रसार

जब किस संख्या का अन्य संख्या में भाग दिया जाता है तो भागफल दो प्रकार का प्राप्त होता है। इन संख्याओं का दशमलव प्रसार (Decimal Expansion of Rational Number) या तो सांत दशमलव प्रसार होता है या असांत आवर्ती दशमलव प्रसार होता है। एक परिमेय संख्या का सांत दशमलव प्रसार कब होता है और कब यह असांत आवर्ती दशमलव प्रसार होता है।

प्रमेय 1 

यदि x एक परिमेय संख्या है जिसका दशमलव प्रसार सांत है, तो x को p/q के रूप में व्यक्त किया जा सकता है, जहाँ p और q सहअभाज्य संख्याएँ हैं और q का अभाज्य गुणनखंड 2ⁿx5^m के रूप का है, जहाँn और m ऋणेतर पूर्णांक संख्याएँ हैं।

1. 3³/2x5² = 27/2x5²

अंश और हर को 2 से गुणा करने पर

= 27x2/2x2x5²

= 54/2²x5²

= 54/(2x5)²

= 54/(10)²

= 54/100

= 0.54 अथवा 0.540

प्रमेय 2 

यदि x, p/q के रूप की एक ऐसी परिमेय संख्या है, कि q का अभाज्य गुणनखंड 2ⁿx5^m के रूप का है, जहाँ n और m ऋणेतर पूर्णांक संख्याएँ हैं, तो x का दशमलव प्रसार, सांत दशमलव प्रसार होता है।

प्रमेय 3

यदि x, p/q के रूप की एक ऐसी परिमेय संख्या है, कि q का अभाज्य गुणनखंड 2ⁿx5^m के रूप का नहीं है, जहाँ n और m ऋणेतर पूर्णांक संख्याएँ हैं, तो x का दशमलव प्रसार, असांत आवर्ती दशमलव प्रसार होता है।

संख्या पद्धति के महत्वपूर्ण सूत्र ( Number System Important Formulas)

• प्रथम n प्राकृतिक संख्याओं का योग Sn_E = n (n + 1)/2 होता है।
• प्रथम n सम संख्याओं का योग S_E = n (n + 1) होता है।
• प्रथम n विषम संख्याओं का योग S₀ = n² होता है।
• किसी भी पहाड़े का योग उस संख्या के पहाड़े के 55 गुने के बराबर होता है।
   उदाहरण- 2 के पहाड़े का योग- 2+4+6+8+10+12+14+16+18+20+ = 110 = 2x 55
   अर्थात् n के पहाड़े का योगफल = 55n
• 1 से n तक के पहाड़े का योगफल = 55 [n (n + 1 )/2]
• प्राकृतिक संख्याओं के वर्गों का योगफल अर्थात् 1² + 2² + 3² + ... + n²= n/6(n + 1) (2n + 1) होता है।
• n प्राकृतिक संख्याओं के घनों का योगफल अर्थात् 1³ + 2³ + 3³ + 4³ + ... +n³ = [n (n + 1)/2] ² होता है।
• n प्राकृतिक सम संख्याओं के वर्गों का योगफल अर्थात् 2² + 4² + 6 ²+ . . . + n2 = 2n/3(n + 1 ) ( 2n + 1)
• n प्राकृतिक सम संख्याओं के घनों का योगफल अर्थात् 2³ + 4³ + 6³ + ... + n³ = 2n² (n + 1)² 

विभाज्यता के नियम  क्या होते हैं? 

विभाज्यता के नियम  (Divisibility Rules)

👉कोई भी संख्या 2 से पूर्णतः विभाज्य होगी, जब उसका इकाई का अंक 0, 2, 4, 6, या 8 होगा।

👉कोई भी संख्या 3 से पूर्णतः विभाज्य होगी, जब उस संख्या के अंकों का योग 3 से पूर्णतः विभाज्य होगा।

👉कोई भी संख्या 4 से पूर्णतः विभाज्य होगी, जब उसके अन्तिम दो अंकों से बनी संख्या 4 से विभाजित हो या अन्तिम दोनों अंक शून्य हो।

👉कोई भी संख्या 5 से पूर्णतः विभाज्य होगी, जब उसका इकाई का अंक 0 या 5 होगा।

👉कोई भी संख्या 6 से पूर्णतः विभाज्य होगी, जब वह संख्या सम संख्या होगी और उसके अंको का योग 3 से विभाज्य हो।

👉कोई भी संख्या 7 से पूर्णतः विभाज्य होगी

• यदि किसी संख्या में लगातार 3 बार 2 समान अंक आए जैसे- 626262,383838
• यदि संख्या इकाई के अंक को दोगुना करके, संख्या के इकाई के अंक को हटाकर प्राप्त हुई संख्या से घटाने पर 7 गुणज मिलता है।

उदहारण: क्या 348 '7' से विभाज्य है? 

स्टेप1: अंतिम अंक हटा दीजिये जो की 8 है। अब संख्या बचती है 34
स्टेप2: अब 8 को डबल करने पर 16 मिलता है और अब 34 में से 16 घटा दीजिये। 34 - 16 = 18 और 18 '7' से विभाज्य नहीं है, इसलिए 348 भी 7 से विभाज्य नहीं है। 

• जब किसी संख्या का 6 बार, 12 बार, 18 बार....... पुनरावृति हुआ, तो वह संख्या 7 से पूर्णतः विभाज्य होगी।

👉जब किसी संख्या के अन्तिम तीन अंक शून्य हों अथवा अंतिम तीन अंकों से बनी संख्या 8 से पूर्णतया विभाजित हो, तो वह 8 से पूर्णतः विभाज्य होगी।

👉कोई भी संख्या 9 से पूर्णतः विभाज्य होगी, जब उस संख्या के अंकों का योग 9 से विभक्त होगा।

👉कोई भी संख्या 10 से पूर्णतः विभाज्य होगी, यदि उसका इकाई का अंक 0 हो।

👉यदि किसी संख्या के विषम स्थानों पर स्थित अंकों के योग तथा सम स्थानों के योग का अन्तर या 11 का गुणज है, तो वह संख्या 11 पूर्णतया विभाज्य होगी।

👉यदि किसी संख्या की पुनरावृति सम में हुई हो, तो वह संख्या 11 से पूर्णतः विभाज्य होगी। जैसे-5555 • यदि कोई संख्या 3 और 4 से विभाज्य है, तो वह 12 से पूर्णतः विभाज्य होगी।

👉यदि किसी संख्या के अंतिम दो अंकों से बनी संख्या 25 से विभाज्य है या अन्तिम दोनों अंक शून्य हैं, तो वह संख्या 25 से पूर्णतः विभाज्य होगी।